La loi de Benford vous empêche de frauder en toute liberté

Aujourd’hui, on va apprendre à frauder le fisc. Ouais, carrément, on est des fous chez #ETC. Imaginez-vous un peu à la tête d’une multinationale. Vous n’êtes pas très honnêtes dans l’âme et, toute l’année durant, vous vous êtes remplis les fouilles avec l’argent de la société. Sachez-le, vous avez tout mon soutien. Après tout, c’est la crise pour tout le monde et il faut bien réussir à payer le crédit de son hôtel particulier parisien et de sa Mazeratti flambant neuve.
Vous êtes malhonnête, c’est une chose, mais tâchez maintenant d’être intelligent. C’est l’heure du bilan comptable et il va bien falloir réussir à truquer les comptes le plus discrètement possible…
Qu’à cela ne tienne! N’écoutant que votre courage, vous vous emparez du bilan comptable annuel (non sans avoir viré votre comptable au préalable, cela va de soi – il aurait été capable de vous dénoncer auprès des actionnaires, le con) et vous vous mettez à changer tous les chiffres pour retomber sur vos pattes. Votre stratégie est parfaitement rodée. Vous avez une explication valable pour TOUTES les lignes de dépenses et vous avez mis sur pied un baratin digne des plus grands interprètes de la Comédie Française.
Autant vous dire que l’inspecteur des Impôts, vous n’allez en faire qu’une bouchée!
Le devoir accompli, vous vous assoupissez l’esprit serein dans votre lit King Size, non sans avoir déposé un bisou plein d’amour sur les lèvres de votre épouse adorée. À ce moment précis, vous êtes persuadé d’être le Roi du monde et que rien ni personne n’arrêtera votre ascension sociale.
Hum. Hum.
Je me pose une question. Avez-vous pensé à la loi de Benford avant de vous ruer tête baissée sur vos falsifications?
Non?
Aïe aïe aïe…
La loi de Benford, la loi mathématique la moins intuitive du monde
Prenons une liste de nombres quelconques, par exemple ceux qui composaient le bilan financier de votre société avant que vous ne commenciez à la falsifier, et analysons les premiers chiffres de chaque nombre.
(et QUE les premiers chiffres de chaque nombre, appelé « chiffre significatif ». Ainsi, sur la liste des nombres 28, 891, 4.657, 214.751 et 17, nous n’analysons que, respectivement, les chiffres 2, 8, 4, 2, et 1.)
(Vous suivez toujours?)
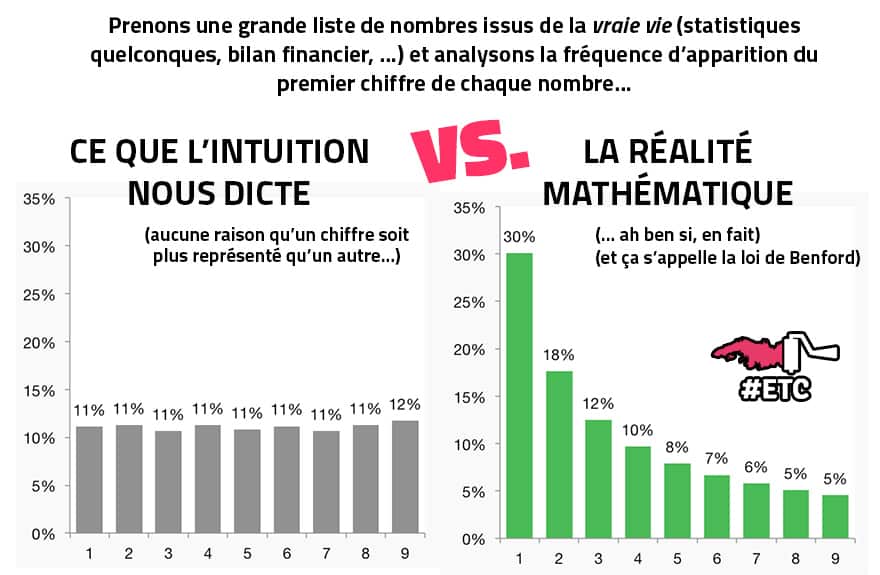
Vous pensez sans doute qu’il y a autant de nombres qui commencent par un 1 que par un 4, ou encore par un 6. Dis plus clairement, si on isole le premier chiffre de tous les nombres composant votre bilan financier, il devrait y avoir en moyenne 11.1% (1 sur 9) de 1, 11.1% de 2, 11.1% de 3, etc… A priori, il n’y a aucune raison pour qu’un chiffre apparaisse plus fréquemment qu’un autre.
Cela semble logique, et, d’ailleurs, pourquoi cela en serait-il différemment?
AB-SO-LU-MENT logique.
Pourtant, ce raisonnement est TOTALEMENT faux!
(et on se rend compte qu’il faut se méfier de ses intuitions en maths.)
Benford (1883 – 1948) est un ingénieur américain qui fit le constat d’une chose tout à fait étonnante. Il s’est rendu compte que dans une liste de nombres, quelque soit le domaine considéré, le chiffre significatif (c’est-à-dire le premier chiffre d’un nombre) le plus fréquent est TOUJOURS le 1! La fréquence d’apparition du 1 est exactement de 30.1%, contre par exemple 5.8% pour le 7 ou 4.5% pour le 9.
(ça marche avec votre dernier relevé bancaire, le ticket de caisse de vos dernières courses, la liste des longueurs des rivières françaises ou même les statistiques sur la fréquentation touristique du Turkménistan)
(bien sûr, il faut quand même que votre liste possède suffisamment de nombres pour être représentative)
(genre avec une liste de 4 ou 5 nombres ça marche pas. Mais avec une liste de plusieurs centaines ou milliers de nombres, ça marche)
C’est plus clair avec un beau dessin:
Mon niveau en mathématiques n’étant pas assez élevé pour procéder à une démonstration de cette bizarrerie mathématique, je laisse le soin à des gens beaucoup plus intelligents que moi de vous l’expliquer, par exemple ici.
(si ce genre de trucs te file la nausée, n’essaye même pas:)
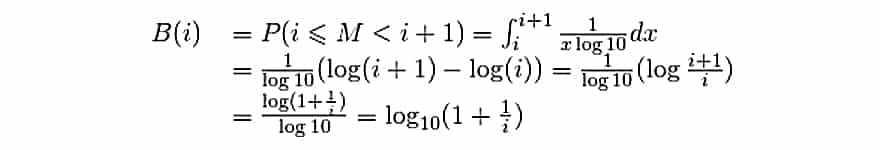
(je t’aurais prévenu)
Pourquoi je vous raconte tout ça, à vous le gérant de société qui venez de falsifier vos comptes? Eh bien, sachez, cher ami, que l’administration fiscale a très bien compris cette loi et qu’elle a mis au point un procédé très simple et rapide pour détecter les fraudeurs!
Il lui suffit de récupérer l’ensemble des nombres rentrés dans un bilan comptable et d’analyser la fréquence d’apparition du premier chiffre de chaque nombre. Si leur distribution statistique ne suit pas la loi de Benford, bingo! Il y a fort à parier qu’il y a anguille sous roche et un inspecteur peu sympathique se fera une joie de le démontrer en poussant ses investigations…
La raison est simple: dans des données falsifiées, on constate que les chiffres 5 et 6 prédominent toujours (les 5 apparaissent environ 40 % du temps et les 6, environ 20 %). Ici, ce n’est pas une « loi » mathématique à proprement parler, mais seulement la faute à notre cerveau qui ne sait pas générer une suite de nombres de façon « naturelle ». Gageons que si le 5 est toujours largement sur-représenté, c’est parce que l’esprit humain essaye de « couper la poire en deux » pour tenter de passer incognito…

L’histoire ne dit pas combien de petits malins se sont fait choper à cause de ce satané Benford!
Si on peut même plus frauder sans être bon en maths, j’vous jure…
____________________________________
Vous avez aimé cet article ? Alors j'ai besoin de vous ! Vous pouvez soutenir le blog sur Tipeee. Un beau geste, facile à faire, et qui permettra à EtaleTaCulture de garder son indépendance et d'assurer sa survie...
Objectif: 50 donateurs
Récompense: du contenu exclusif et/ou en avant-première
Je vous remercie pour tout le soutien que vous m'apportez depuis maintenant 5 ans, amis lecteurs!
Djinnzz
PS: ça marche aussi en cliquant sur l'image juste en dessous ↓↓↓↓











Je trouve que vous n’avez pas insisté sur les limitations de cette loi. Par exemple, si vous prenez les notes d’un bulletin d’un bon élève, le pourcentage du 1 s’approche fortement 100% (en admettant qu’il ait la moyenne dans quasi toutes les matières).
En réalité, il faut que la répartition soit réellement aléatoire.
Et la raison pour laquelle si un cerveau humain dresse une liste aléatoire de nombres la loi de Benford n’est pas appliquée, c’est simplement parce que le cerveau humain n’est pas capable de générer un vrai tirage aléatoire. Un algorithme peut donc facilement déterminer s’il y a fraude on non.
Il existe effectivement des limites à la loi de Newcomb-benford.
Cependant, la distribution des nombres dans votre exemple est de fait faussée parla césure à la note maximale (20). C’est-à-dire qu’il faudrait raisonner sur les seconds chiffres non nuls en utilisant la loi généralisée.
Woaw fascinant :O
Merci pour avoir illuminé ma pause café (enfin plutot mon déjeuner ce qui en soit est une pause dans ma nuit)
Et je rassure tout le monde, pas besoin d’être bac+12 pour comprendre cet aperçu de démo 😀 [Aucune idée du niveau en France mais avoir fait une année ou deux d’université en Belgique aide quand meme grandement a comprendre :p]
C’est vraiment TRES étonnant ce résultat.
Même si j’imagine que la démonstration mathématique tient la route, je n’arrive pas à me l’expliquer. Pourquoi, si une liste de nombres est générée aléatoirement, y aurait-il plus de 5 que de 7? Plus de 1 que de 3?
Très très bizarre ce truc…
Et pourtant…
Hello, justement, les nombres ne sont pas générés « aléatoirement », avec une suite de nombres aléatoires, la loi de Benford ne marche pas, et tu auras bien tes « 11% » pour chacun.
Ton ticket de caisse, la taille des fleuves etc. ne sont pas aléatoires mais répondent à des logiques financière et physique.
Sans rentrer dans les détails, la démonstration explique que pour arriver à 6, tu passes par 1, 2, 3, 4 et 5. Or, on va dire qu’il y a une petite chance pour que tu « t’arrêtes » avant. Alors que pour aller à 1, tu « passes » par aucun autre nombre.
La conclusion de l’article mentionné vous donne une réponse à votre question:
« La loi de Benford est fascinante: elle défie l’intuition, et c’est quelque chose que vous pouvez tester vous-même et adapter à une activité en classe. Il s’agissait d’une curiosité, mais c’est maintenant un outil standard pour détecter les fraudes. Bien sûr, de plus en plus de fraudeurs en entendent parler. Mais faites attention: le premier chiffre n’est pas la seule chose à laquelle il faut faire attention. La loi de Benford généralisée permet de créer une loi pour le second chiffre, le troisième, etc. Vous pouvez essayez de le trouver vous-même: demandez-vous simplement dans quelles unions d’intervalles la mantisse d’un nombre doit être de sorte que son second chiffre soit i. »
En gros, c’est contre-intuitif, et pour avoir fait beaucoup de maths dans ma jeunesse, je peux vous dire que l’intuition est le plus ennemi du mathématicien.
La seule façon d’expliquer clairement ce résultat est de se plonger dans les maths, les probas, les logarithmes et les intégrales de fonctions. J’ai suivi en diagonale la démonstration proposée et elle m’a l’air rigoureuse.
La remarque sur le deuxième, le troisième, etc. chiffre me fait bien plaisir: c’est immédiatement ce à quoi j’ai pensé en lisant l’article. Si une règle régit le premier chiffre non nul d’un nombre (qui s’appelle la mantisse), pourquoi n’y en aurait-il pas pour les autres chiffres?
Par contre, la loi de Benford est très facilement contrable. Il suffit de générer une liste de nombres par Excel qui collent avec elle. Attention, faire générer une liste de nombres aléatoire par un programme informatique ne suffit pas (du moins, je pense) car l’impossibilité d’un programme informatique de générer un « vrai » nombre aléatoire a déjà été démontrée. (l’ « aléatoire » est une notion mathématique également complexe)
D’ailleurs, une petite vérif pourrait être faite rapidement sur Excel: On génère une liste de nombres « aléatoires » avec la fonction rand(), puis on analyse la fréquence d’apparition du premier chiffre de chaque nombre.
Si au final on est loin de la répartition théorique, cela prouve que la fonction rand d’Excel n’est pas si au point que ça…
J’ai la flemme de le faire pour le moment, mais je testerai un jour où je me fais chier 😉
En fait, malgré l’étrangeté de ce résultat, on peut trouver une explication trés logique á son existence. Ne vous laissez pas leurrer par l’apparente folie furieuse que semble reveter le déesse des maths en cette occasion
(Oui, en prépa, on crée nos propres divinitées á vénérer, on en a bien besoin… D’ailleurs, Algorithma est extrémement capricieuse et cruelle: en dessous d’un nombre exponentiel d’heures de votre vie sacrifiées á l’étude de ses mystéres divins, elle ne vous accordera jamais ses faveurs et vous maudira de la terrible Tuaurajamaisplusdequatreatesinterros!!!, la malédiction la plus horrible que peut subir un étudiant…)
si vous prenez le nombre 1, il faut y ajouter la totalité de sa valeur pour passer au nombre suivant, 2. á ce dernier il suffit d’ajouter la moité de sa valeur pour passer á 3… et etc, jusqu’á 9, auquel il suffit d’ajouter un neuviéme de sa valeur pour revenir á 1 ( bon, 10, mais le premier chiffre est 1).
Pour un esprit physicien, ce serait comme dire: l’energie nécessaire pour quitter l’état « 9 », relativement á celle dont nous disposons déjá, est beaucoup plus faible que si nous étions dans l’état « 1 ». Donc l’état « 9 » a une durée de vie beaucoup plus faible que celle de l’état « 1 ». On l’aperçoit donc beaucoup plus rarement.
En effet, même avec ce constat, la loi de Benford continue á ressembler á un spectacle de prestidigitation. Mais ce qui est vraiment fascinant et magique avec cette loi, c’est son universalité. Enfin bon, il y a une démonstration trés bonne donné dans cet article, je vous laisse la lire. Elle explique tout ça beaucoup mieux que moi.
Oui, c’est super comme explication le coup du passage d’un chiffre à l’autre.
Ca se traduit comme ça, non?
i+1 = i + 1/i
Merci !
i + 1 = i + i/i
Oui, ou pour mettre en évidence l’effort pour quitter i (sur une base 100) :
(i + 1) = (i + i/i) = i + (100% / i) = i + (100/i)%
Donc :
– pour quitter 1, il faut un effort de 100/1 = 100
– pour quitter 2, il faut un effort de 100/2 = 50
– pour quitter 3… 33,3
…
– pour quitter 9… 11,1
Génial! C’est une propriété qui n’est pas du tout intuitive et j’ai mal à la tête rien qu’à essayer de chercher un début d’explications (je sais pourquoi je n’aimais pas les maths au lycée!)
Le pauvre chef d’entreprise qui tente de frauder dans ses bilans comptables ne doit pas comprendre ce qui lui arrive quand un contrôle fiscale lui tombe sur le coin de la gueule! (et il se demandera surement toute sa vie pourquoi, ô oui pourquoi c’est justement son entreprise qui s’est fait contrôler!) Eh oui, qui penserait que les mathématiques pourraient trahir notre malhonnêteté?
Totalement fou, totalement contre-intuitif!
J’ai beau me triturer le cerveau dans tous les sens je n’arrive pas à comprendre POURQUOI cette règle est vérifiée!
Puisque la liste des nombres est aléatoire, le premier chiffre de chaque nombre est lui aussi aléatoire, donc POURQUOI le 1 sort-il 6 fois plus souvent que le 9???
Je ne peux que faire confiance aux esprits plus brillants que moi qui l’ont démontré, mais quand même, CA M’ENERVE!!!!
Après deux ans de réflexions pour chercher à comprendre, je jette ma craie et replie les volets de mon tableau vert (non, pas noir, on est moderne !) Ensuite, on se plonge dans la mythologie ou dans l’histoire des Pharaons. Et enfin, on respire le plus calmement du monde… !! (et surtout, on oublie…)
Ah ah !!